Borbin the 🐱

For Math126 we were talking about the Taylor series for

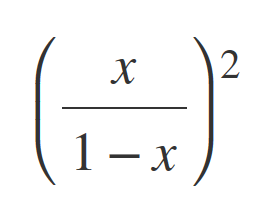
It looks difficult at first glance, but it is actually quite simple. Let me explain:

Using this as a base:

The derivative of this term is:

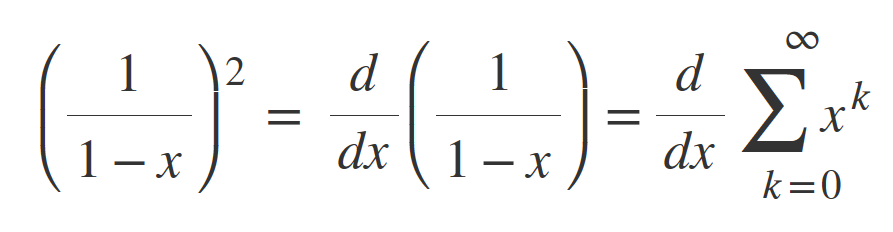
Which gets to:

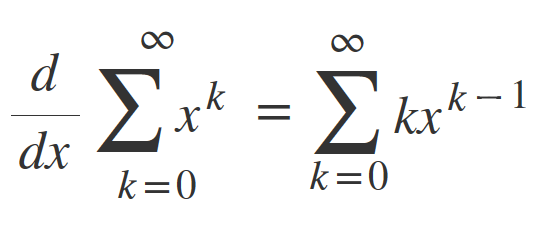
Now move the nominator in the sum to get the solution:

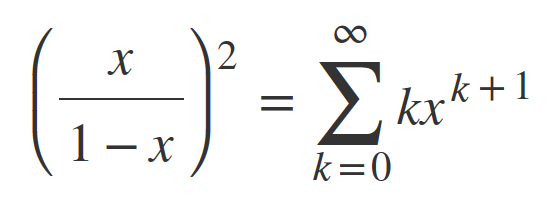
Time for a small PowerShell script for the Taylor series:

function f([double]$x)
{
    [Math]::Pow($x/(1-$x), 2)
}

function T([double]$x, [int]$k)
{
    0..$k | % { $sum = 0 } { $sum += $_ * [Math]::Pow($x, $_ + 1) } { $sum }
}


[int]$K = 16

for([int]$xi = -5; $xi -le 5; $xi += 1)
{
    [double]$x = $xi / 10

    [PSCustomObject]@{
        'x' = $x
        'f(x)' = f $x
        'T(x)' = T $x $K
    }
}

   x                f(x)                T(x)
   -                ----                ----
-0,5   0,111111111111111   0,111068725585938
-0,4  0,0816326530612245  0,0816318326348185
-0,3  0,0532544378698225  0,0532544328723274
-0,2  0,0277777777777778  0,0277777777741005
-0,1 0,00826446280991736 0,00826446280991734
   0                   0                   0
 0,1  0,0123456790123457  0,0123456790123457
 0,2              0,0625  0,0624999999943475
 0,3   0,183673469387755   0,183673459741776
 0,4   0,444444444444445   0,444442421037629
 0,5                   1   0,999862670898438

The convergence is | x | < 1
T₁₅ is used for this test.

 k             Tk(x)
 -             -----
 0                 0
 1              0,25
 2               0,5
 3            0,6875
 4            0,8125
 5          0,890625
 6            0,9375
 7        0,96484375
 8        0,98046875
 9      0,9892578125
10       0,994140625
11    0,996826171875
12    0,998291015625
13  0,99908447265625
14     0,99951171875
15 0,999740600585938